Grant 0794/2020 "Spectral Methods in Hyperbolic
Geometry"
Identifier: PN-III-P4-ID-PCE-2020-0794
Period: 2021-2023.
Financed by: ANCS-UEFISCDI contract
117/2021
Budget: 1198032 lei
Grant director: Sergiu Moroianu
Team members:
Liana David (experienced researcher)
Cezar Oniciuc (experienced researcher)
Costin Vîlcu (experienced researcher)
Cipriana Anghel (PhD student)
Rareş Stan (PhD student)
Dragoş Manea (Master student)
Rezumat.
Spatiul de moduli de suprafete Riemann este intim legat de geometria
hiperbolica. Metrica Riemann pe acest spatiu este definita de produsul scalar
L^2 fata de unica metrica hiperbolica dintr-o clasa conforma. Mai mult, forma
Kähler pe partea regulata a spatiului de moduli admite diverse potentiale Kähler
pe acoperirea universala in sens orbifold, adica pe spatiul Teichmüller. Unul
dintre aceste potentiale este determinantul Laplacianului fata de metrica
hiperbolica. Un altul este volumul renormalizat al unei metrici hiperbolice pe o
3-varietate de volum infinit care corespunde unui cobordism hiperbolic in
dimensiune 2+1. Vom extinde aceste obiecte - si rezultate - la frontiera
spatiului Teichmüller. Vom investiga determinantul operatorului Dirac pe
suprafete hiperbolice, limita sa adiabatica (colapsarea unei familii de
geodezice simple disjuncte) si sa construim in acest fel un potential Kähler
care se extinde continuu la unele din componentele de bord, adica la spatiilor
Teichmüller ale suprafetelor punctate. Este cunoscut ca determinantul
Laplacianului devine singular la toate fetele de bord ale spatiului Teichmüller
space corespunzatoare limitei adiabatice. Anticipam ca formula de urma Selberg
va juca un rol in analiza noastra, dar intentionam de asemenea sa folosim
algebre de operatori pseudodiferentiali adaptate acestei limite geometrice,
pentru a controla nucleul Schwartz al puterilor complexe ale operatorului Dirac.
Abstract.
The moduli space of Riemann surfaces is intimately related to hyperbolic geometry. The Riemann metric on this space is defined by the scalar product L^2 with respect to the only hyperbolic metric in a conformal class. Moreover, the Kähler form on the regular part of the moduli space admits various Kähler potentials on the universal covering in the orbifold sense, i.e. on the Teichmüller space. One of these potentials is the determinant of the Laplacian against the hyperbolic metric. Another is the renormalized volume of a hyperbolic metric on a 3-manifold of infinite volume that corresponds to a hyperbolic cobordism in dimension 2+1. We will extend these objects - and results - to the frontier of Teichmüller space. We will investigate the determinant of the Dirac operator on hyperbolic surfaces, its adiabatic limit (the collapse of a family of simple disjoint geodesics) and in this way construct a Kähler potential that extends continuously to some of the board components, i.e. to the Teichmüller spaces of the dotted surfaces. It is known that the determinant of the Laplacian becomes singular at all edges of the Teichmüller space corresponding to the adiabatic limit. We anticipate that the Selberg trace formula will play a role in our analysis, but we also intend to use algebras of pseudo-differential operators adapted to this geometric limit, to control the Schwartz kernel of complex powers of the Dirac operator.
Activity
Significant results
Our results improve the understanding of the moduli spaces of Riemann surfaces of finite volume. Each compact Riemann surface, together with a topological choice of a spin structure, determines an entire function Z(s), called the Selberg zeta function, displaying a symmetry around $s=1/2$ like the famous Riemann zeta function. The value at s=1/2 is of particular interest since it is related to the "determinant" of the Dirac operator. By one of the results of our project, the family of Selberg zeta functions, so in particular the central value, have a limit after renormalization by a constant factor when the Riemann surface "degenerates'' along a simple closed curve.
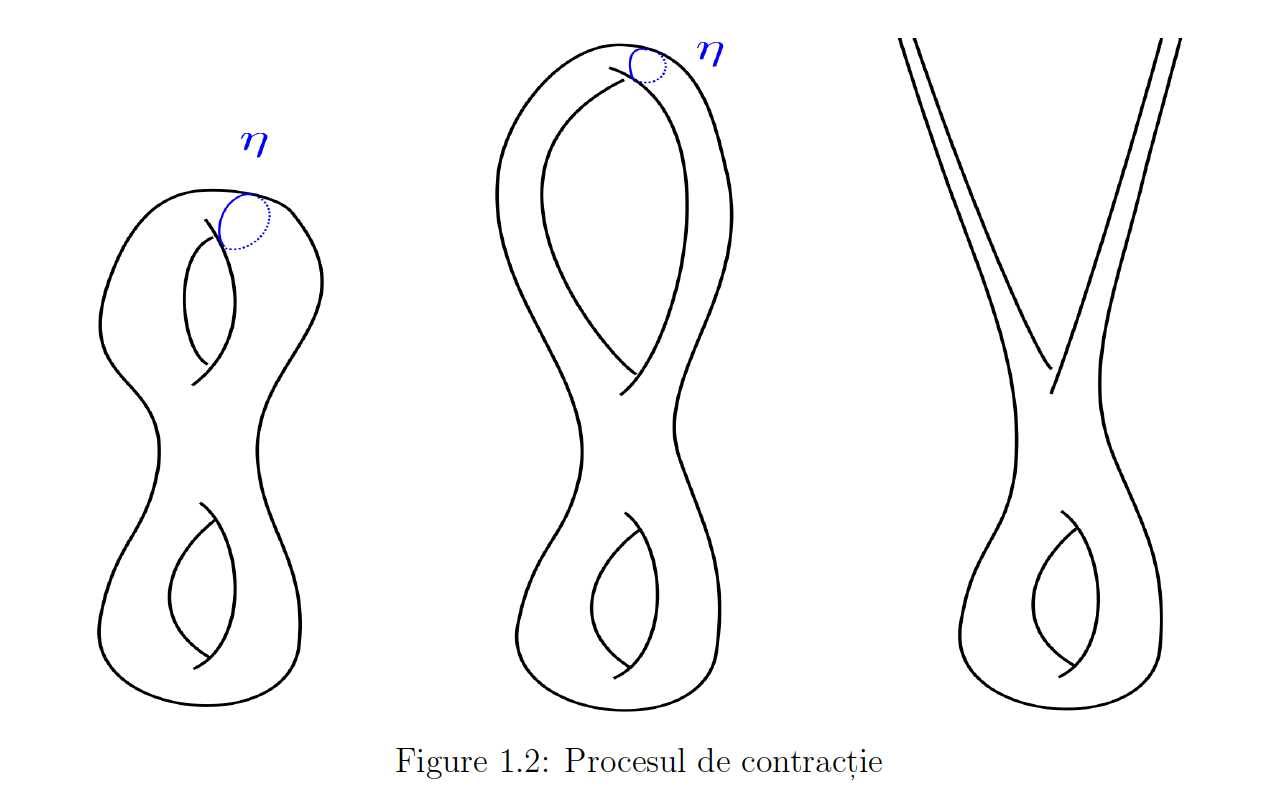
At the limit, we obtain a noncompact hyperbolic Riemann surface with two cusps. We proved that this noncompact surfaces also admits a Selberg zeta function, which equals the renormalizd limit of the zeta functions of the degenerating surfaces.
Report
Raport 0794 final
Publications
R. Stan, "Spectral convergence of the Dirac operator on typical hyperbolic surfaces of high genus", arXiv:2307.01074
J. O'Rourke, C. Vîlcu, "Reshaping Convex Polyhedra", Research monograph to be published by Springer-Verlag in 2024. 239 pages, 125 figures, 133 references, ISBN 978-3-031-47510-8.
arXiv:2107.03153.
J. O'Rourke, C. Vîlcu, "Cut locus realizations on convex polyhedra",
Computational Geometry: Theory and Applications Vol. 114, No. C (2023), 102010, https://doi.org/10.1016/j.comgeo.2023.102010.
V. Branding, S. Montaldo, C. Oniciuc, A. Ratto, "Polyharmonic hypersurfaces into pseudo-Riemannian space forms",
Annali di Matematica Pura ed Applicata, (4) 202 (2023), no.2, 877-899, DOI10.1007/s10231-022-01263-1
Maria Del Mar González, Liviu Ignat, Dragoş Manea, Sergiu Moroianu
"Concentration limit for non-local dissipative convection-diffusion kernels on the hyperbolic space",
[pdf],
arXiv:2302.02624.
R. Stan, "The Selberg trace formula for spin Dirac operators on degenerating hyperbolic surfaces", preprint arXiv:2212.11793.
C. Cazacu, L. Ignat, D. Manea, "The Hardy inequality and large time behaviour of the heat equation on R^{N-k}x(0,\infty)^k",
Journal of Differential Equations 375 (2023) 682-705, DOI 10.1016/j.jde.2023.09.007, arxiv.org/abs/2211.08828.
D. Fetcu, C. Oniciuc, "Biharmonic and biconservative hypersurfaces in space forms", Differential geometry and global analysis - in honor of Tadashi Nagano, 65--90, Contemp. Math., 777, Amer. Math. Soc., [2022],
DOI: https://doi.org/10.1090/conm/777/15628
C. Anghel, "Heat kernel asymptotics for real powers of Laplacians", published online in Canadian Journal of Mathematics, preprint arXiv:2203.14142.
Montaldo, S.; Oniciuc, C.; Ratto, A.; "On the second variation of the biharmonic Clifford torus in S^4", Ann. Global Anal. Geom. 62 (2022), no. 4, 791--814.
DOI: https://doi.org/10.1007/s10455-022-09869-7
V. Cortés, L. David, "B_n-generalized pseudo-Kähler structures", J. Geom. Analysis (2023), 33:261,
https://doi.org/10.1007/s12220-023-01311-z,
arxiv:2206.10456.
V. Branding, S. Montaldo, C. Oniciuc, and A. Ratto,
"Unique continuation properties for polyharmonic maps between Riemannian manifolds",
Canad. J. Math. 2021, pp. 1-28, http://dx.doi.org/10.4153/S0008414X21000420
B. Flamencourt, S. Moroianu, "Cauchy spinors on 3-manifolds", J. Geom. Analysis 32 (2022), art. 186, arXiv:2011.06538, DOI: 10.1007/s12220-022-00925-z.
J. O'Rourke, C. Vîlcu: "Simple Closed Quasigeodesics on Tetrahedra",
Information 2022, 13(5), 238.
S. Moroianu, "Higher transgressions of the Pfaffian", Revista Matemática Iberoamericana 38 (2022), no. 5, 1425-1452, arXiv:2011.06538.
J. O'Rourke, C. Vîlcu: "Cut Locus Realizations on Convex Polyhedra", arXiv:2102.11097,
Proc. CCCG 21, 279-285.
V. Cortés, L. David, "T-duality for transitive Courant algebroids",
arxiv:2101.07184, J. Symplectic Geom. 21, no. 4 (2023)
S Montaldo, C Oniciuc, A Ratto, "Polyharmonic hypersurfaces into space forms",
Israel J. Math. 249 (2022), no. 1, 343--374,
DOI: 10.1007/s11856-022-2315-5
C Anghel, R Stan, "Uniformization of Riemann surfaces revisited", Annals of Global Analysis and Geometry 62 (2022), 603-615, DOI: 10.1007/s10455-022-09860-2.
Conferences organized
Differential Geometry Workshop 2023,
Alexandru Ioan Cuza University Iaşi, organizing committee: Volker Branding, Razvan Litcanu, Cezar Oniciuc, Sept. 06 - 09 2023.
Semiclassical limits of modes and quasi modes, Paris, France, scientific committee: Gilles Courtois, Julien Marché, Sergiu Moroianu, 13 - 18.11.2022.
Differential Geometry Workshop 2022,
University of Vienna, scientific committee: Cezar Oniciuc, Eric Loubeau, Andrea Ratto, Sept. 07 - 09 2022.
Semiclassical trace formula, Paris, France, scientific committee: Gilles Courtois, Julien Marché, Sergiu Moroianu, Nov. 15 - 19, 2021.
Organizations of Seminars
C. Anghel, weekly seminar on "b-Calculus and pseudodifferential operators".
R. Stan, weekly seminar on "Brownian motion to Black-Scholes".
Invited talks
C. Anghel, "Non-local coefficients in the heat asymptotics for real powers of Laplacians", University of Göttingen, 24 - 28.04.2023.
R. Stan, "The Selberg trace formula for spin Dirac operators on degenerating hyperbolic surfaces", University of Göttingen, 24 - 28.04.2023.
R. Stan, "Uniformization of Riemann surfaces revisited", University of Bristol, 28.02.2023.
R. Stan, "Selberg zeta function for the Dirac operator on degenerating hyperbolic
surfaces", University of Regensburg, 22.07.2022.
L David, ''Generalized pseudo-Kahler structures of type B_n I", Geometry seminar, IMAR, Bucharest, 5.07.2022
L David, ''Generalized pseudo-Kahler structures of type B_n II", Geometry seminar, IMAR, Bucharest, 18.10.2022
C. Vîlcu, "Simple Closed Quasigeodesics on Tetrahedra", IMAR Geometry Seminar, 24.05.2022
L David, "T-duality for transitive Courant algebroids", Utrecht Geometry
Center, (Olanda), 26.03.2021
S Moroianu, "Higher transgressions of the Pfaffian",
Geometry and Topology seminar, University of Luxemburg, 28.09.2021.
S Moroianu,"The Gauss-Bonnet formula on Riemannian polyhedra via higher transgressions of the Pfaffian",
Théorie de Lie, Géométrie et Analyse seminar,
Université de Lorraine, 30.09.2021.
Scientific visits
Victor Nistor (Metz, France) visited IMAR, 21 - 28.10.2023
Adrien Boulanger (Marseille, France) visited IMAR, 24 - 28.10.2023
Léo Bénard (Universität Göttingen, Germany) visited IMAR, 10 -
13.06.2023
S Moroianu visited Université de Rouen, France, 04 - 06.06.2023
Andrei Moroianu (Orsay, France) visited IMAR, 20.04 - 01.05.2023
R. Stan visited the University of Bristol, 27.02 - 03.03.2023.
C. Anghel visited the University of Geneva, 01 - 11.04.2022.
R. Stan visited the University of Geneva, 01 - 11.04.2022.
Andrei Moroianu (Orsay, France) visited IMAR, 17.03 - 02.04.2021
Adrien Boulanger (Bologna, Italy) visited IMAR, 24.04 - 17.05.2021
Richard Horja (Miami, SUA) visited IMAR, 29.08 - 04.09.2021.
Dirk Frettlöh (Bielefeld, Germania) visited IMAR, 29.08 - 03.09.2021.
S Moroianu, Université de Lorraine, Metz, France, 13.09 - 08.10.2021
C Anghel, University of Geneva, 1 - 14.11.2021.
R Stan, University of Geneva, 1 - 14.11.2021.
Andrei Moroianu (Orsay, France) visited IMAR, 18.11 - 06.12.2021
Participation in conferences/summer schools
S. Moroianu presented "Localization of random Schrödinger operators on graphs using fractional moments of Green operators" at
Anderson Localization, Auffargis, France, 14 - 18.11.2023.
S. Moroianu presented "Gauss-Bonnet formulae on noncompact manifolds" at the conference
"Geometry beyond Riemann: Curvature and Rigidity", ESI Vienna, 16 - 20.10.2023
S. Moroianu presented "The Gauss-Bonnet formula on polyhedral manifolds" at the conference "Prospects in Geometry and Global Analysis", Rauischholzhausenschloss, Germany, 21 - 25.08.2023
D. Manea presented "Concentration limit for non-local dissipative convection-diffusion kernels on the hyperbolic space'' at the 10th Congress of Romanian Mathematicians, Piteşti, 30.06-5.07.2023.
C. Vîlcu presented ''Reshaping convex polyhedra'' at the 10th Congress of Romanian Mathematicians, Piteşti, 30.06-5.07.2023.
L David presented ''B_{n}-Generalized Pseudo-Kähler Structures'' at the 10th Congress of Romanian Mathematicians, Piteşti, 30.06-5.07.2023.
C. Anghel attended "The Tenth Congress of Romanian Mathematicians", Piteşti, 30.06.2023-05.07.2023.
R. Stan attended "The Tenth Congress of Romanian Mathematicians", Piteşti, 30.06.2023-05.07.2023.
S. Moroianu presented ``Microlocalization of quantum measures" at Arithmetic quantum unique ergodicity, Cap Ferret, France, 12 - 16.16.2023.
C. Anghel presented ``Microlocal lifts of quantum measures on compact hyperbolic surfaces" at Arithmetic quantum unique ergodicity, Cap Ferret, France, 12 - 16.16.2023.
D. Manea presented "Concentration limit for non-local dissipative convection-diffusion kernels on the hyperbolic space'' at the conference "Nonlocal Equations: Analysis and Numerics", Bielefeld, Germania, 06 - 10.03.2023.
C. Anghel presented "Non-local coefficients in the heat asymptotics for real powers of Laplacians"
at Aussois Winter School, Aussois, France, 11 - 16.12.2022.
R. Stan attended "Aussois Winter School", Aussois, France, 11 - 16.12.2022.
R. Stan presented "Uniform Weyl's law on degenerating surfaces" at Random walks and related random topics, University of Goettingen, 17 - 21.10.2022.
R. Stan presented "Valori proprii ale suprafetelor hiperbolice" at A XXIV-a Conferinta anuala a SSMR, Universitatea Politehnica, 28.10.2022.
C. Anghel presented "Hassel's construction of semiclassical measures in the stadium" at
Semiclassical limits of modes and quasi modes, Paris, France, 13 - 18.11.2022.
C. Anghel presented "Non-local coefficients in the heat asymptotics for real powers of Laplacians" at Young Women in Geomtric Analysis, Bonn, Germany, 27-29.06.2022.
C. Anghel presented "Non-local coefficients in the heat asymptotics for real powers of Laplacians" at Analytic and Geometric Aspects of Spectral Theory, Oaxaca, Mexico, 15-19.08.2022 (online).
C. Anghel presented "Heat kernel asymptotics for real powers of Laplacians" at Doctoral
Research Days Workshop, IMAR, Bucharest, 11-12.10.2022 (online).
C.Anghel presented "Heat kernel asymptotics for real powers of Laplacians" at Random
Walks and related random topics, Gottingen, Germany, 17-21.10.2022.
C.Anghel presented "Functia Zeta-Epstein si nucleul caldurii" at A XXIV-a Conferinta
anuala a SSMR, Universitatea Politehnica, Bucharest, 28.10.2022.
S. Moroianu presented "Counterexamples to Unique Quantum Ergodicity" at
Semiclassical limits of modes and quasi modes, France, 14 - 18.11.2022.
D. Manea presented "A Non-local non-linear convection-diffusion problem on metric trees", "Heating up networks - analysis meets applications meeting", 05 - 10 octombrie 2022, Keiserslautern, Germania, \url{https://mat-dyn-net.eu/en/activities/ca18232-heating-up-networks-analysis-meets-applications-workshop}.
D. Manea presented "A Non-local non-linear convection-diffusion problem on the Hyperbolic space" and "A Non-local non-linear convection-diffusion problem on metric trees" at the "IX Partial differential equations, optimal design and numerics", 21 august - 02 septembrie 2022, Benasque, Spania, \url{https://www.benasque.org/2022pde/}
L. David presented ''B_n generalized pseudo-Kahler structures'', at Inaugural Conference 'Edging Higher', International Center for Mathematical Sciences, Sofia, Bulgaria, 10 - 14.07.2022
C. Anghel presented "Shadowing Lemma and Anosov Closing Lemma" at Entropy of semiclassical measures, Les Plantiers, France, 13 - 17.06.2022.
R. Stan presented "Jacobi fields and the Anosov property of the geodesic flow" at Entropy of semiclassical measures, Les Plantiers, France, 13 - 17.06.2022.
S. Moroianu presented "Ergodicity of the geodesic flow" at Entropy of semiclassical measures, Les Plantiers, France, 13 - 17.06.2022.
D. Manea, "A Non-local non-linear convection-diffusion problem on the Hyperbolic space", Workshop for Young Researchers in Mathematics – 11th Edition, 19 mai - 20 2022, IMAR, \url{https://fmi.univ-ovidius.ro/cercetare/wyrm2022/}
C. Anghel attended "Geometry and Analysis on non-compact manifolds", Marseille, France, 28.03.2022-01.04.2022.
R. Stan attended "Geometry and Analysis on non-compact manifolds", Marseille, France, 28.03.2022-01.04.2022.
S. Moroianu attended "Geometry and Analysis on non-compact manifolds", Marseille, France, 28.03.2022-01.04.2022.
C. Anghel presented "Non-local coefficients in the heat asymptotics for real powers of Laplacians", Workshop for Young Researchers in Mathematics (11th Edition), Bucharest, 19 - 20.05.2022.
D. Manea presented "Non-local transport problem on Hyperbolic space", Workshop for Young Researchers in Mathematics (11th Edition), Bucharest, 19 - 20.05.2022.
R. Stan attended "Workshop for Young Researchers in Mathematics" (11th Edition), Bucharest, 19 - 20.05.2022.
R Stan presented "Selberg trace formula on compact manifolds", Workshop for
Young Researchers in Mathematics (10th Edition), Constanta,
20 - 21.05.2021
C Anghel presented "Heat kernel asymptotics for real powers of Laplacians",
Workshop for Young Researchers in Mathematics (10th Edition), Constanta,
20 - 21.05.2021
J O'Rourke, C Vîlcu presented "Cut Locus Realizations on Convex Polyhedra",
33rd Canadian Conference on Computational Geometry (CCCG 2021)}, Canada
(on-line), 10 - 12 august 2021.
C Vîlcu presented "Convexity on Convex Polyhedra",
The 14th International Conference on Discrete Mathematics:
Discrete Geometry and Graph Theory, University of Bucharest, 30.08 -
3.09.2021.
S Moroianu attended
Locally Conformal Symplectic Manifolds: Interactions and Applications",
Banf, Canada, 8 - 12.11.2021.
L David presented "Generalized connections, spinors and T-duality",
ONEW Generalized Connections
and Curvature, Barcelona University (Spain)/University of Hamburg (Germany),
15.11.2021.
C Anghel presented "WKB expansions of solutions of the Schrödinger
equation" at
Semiclassical trace formula,
Paris, France, 15 - 19.11.2021.
R Stan presented "WKB-expensions and applications to the Hamilton-Jacobi
equation" at
Semiclassical trace formula,
Paris, France, 15 - 19.11.2021.
S Moroianu presented "Semiclassical pseudodifferential operators" at
Semiclassical trace formula,
Paris, France, 15 - 19.11.2021.
L David, "T-duality for transitive Courant algebroids",
Special Geometry, Mirror Symmetry and Integrable Systems, Waseda University/RIMS
Kyoto University (Japan), 29.11 - 2.12.2021.
Updated: November 23, 2023
