Contributor: André
Haefliger
June 1999, Boulder |
Question: Let 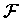 be a foliation on a manifold M such that the universal covering
of each leaf is contractible and T be a transveral. Let G
be the fundamental groupoid of
be a foliation on a manifold M such that the universal covering
of each leaf is contractible and T be a transveral. Let G
be the fundamental groupoid of 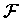 associated with T. Prove that for every G-sheaf
associated with T. Prove that for every G-sheaf 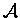 on T, the map
on T, the map
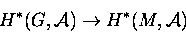
is an isomorphism.
Answer proposed by
Ieke Moerdijk
at January 22, 2001.
|
Contributor: Steve Hurder
June 1999, Boulder |
Question: Let 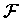 be an amenable C1 foliation on a compact manifold M.
be an amenable C1 foliation on a compact manifold M.
a) If L is a compact leaf, must its holonomy group be amenable?
b) Same question for a dense leaf L. |
Contributor: Jerry Kaminker
June 1999, Boulder
|
Preamble. Let G be a Lie groupoid and 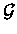 its Lie algebroid. Then we have the pseudo-differential operators extension
its Lie algebroid. Then we have the pseudo-differential operators extension
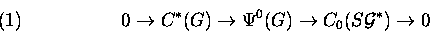
as an element of 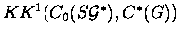 . .
In the case when 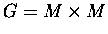 ,
the extension ,
the extension
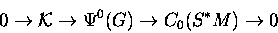
is determined by the symplectic structure of S*M
via the Index Theorem for Families.
Question: What does the Poisson algebra structure of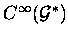 determine about (1) ?
determine about (1) ?
Does it determine the cohomology class needed in a topological index
formula? |
Contributor: Alex Kumjian
June 1999, Boulder |
Question: Find a groupoid cohomology (with coefficients) valid
for locally compact groupoids such that the following conditions are satisfied:
1) Theory agrees with Grothendieck's equivariant sheaf cohomology if
the groupoid is étale.
2) Theory agrees with Moore's cohomology if the groupoid is a locally
compact group.
3) An equivalence of groupoids induces an isomorphism of cohomology.
4) The second cohomology with the circle as coefficients may be identified
with the Brauer group of the groupoid. |
Contributor: Alex Kumjian
June 1999, Boulder
|
Question: Let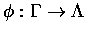 be a continuous open morphism (surjective) between groupoids. Under what
conditions does one get a Fell bundle E over
be a continuous open morphism (surjective) between groupoids. Under what
conditions does one get a Fell bundle E over 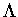 such that
such that 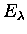 is
the closure of is
the closure of  (under an appropriate norm) and
(under an appropriate norm) and
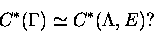
|
Contributor: Paul Muhly
June 1999, Boulder
|
Question: Let G be a principal, étale groupoid.
When does there exist a ``faithful'' 1-cocycle 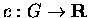 ,
i.e. a continuous homomorphism ,
i.e. a continuous homomorphism 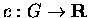 such that c-1(0)=G(0)
? A necessary condition is amenability, but is it sufficient?
such that c-1(0)=G(0)
? A necessary condition is amenability, but is it sufficient? |
Contributor: Chris Phillips
June 1999, Boulder
|
Question: Let G be an amenable étale essentially
principal groupoid. When is Cr*(G)
a stably finite C*-algebra? |
Contributor: Chris Phillips
June 1999, Boulder
|
Question: Let G be an étale groupoid and let X
be a proper G-space. Can K0G(X)
be described using finite dimensional vector bundles only? |
Contributor: Birant Ramazan
June 1999, Boulder
|
Preamble. Suppose that 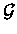 is the Lie algebroid of a Lie groupoid G. Then the tangent groupoid
is the Lie algebroid of a Lie groupoid G. Then the tangent groupoid 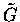 defines a continuous field of C*-algebras
defines a continuous field of C*-algebras 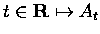 ,
with At=C*(G)
for ,
with At=C*(G)
for 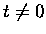 and
and 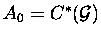 which gives the bracket of the Poisson algebra
which gives the bracket of the Poisson algebra 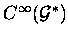 as a limit of commutators.
as a limit of commutators.
For an arbitrary Lie algebroid 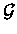 ,
one can only construct a local Lie groupoid G which has ,
one can only construct a local Lie groupoid G which has 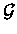 as its Lie algebroid. The construction of the tangent groupoid has been
extended to local Lie groupoids in the context of pseudo-differential operators
by Nistor, Weinstein and Xu. The missing ingredient in order to extend
the above result to an arbitrary Lie algebroid is the construction of the
C*-algebra of a local Lie groupoid.
as its Lie algebroid. The construction of the tangent groupoid has been
extended to local Lie groupoids in the context of pseudo-differential operators
by Nistor, Weinstein and Xu. The missing ingredient in order to extend
the above result to an arbitrary Lie algebroid is the construction of the
C*-algebra of a local Lie groupoid.
Question: Is it possible to extend the usual construction of
the convolution C*-algebra C*(G) to
a local Lie groupoid G ? |
Contributor: Arlan Ramsay
June 1999, Boulder
|
Preamble. Consider the transformation groupoid 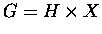 of a smooth action of a Lie group H on a manifold X. Then
for each
of a smooth action of a Lie group H on a manifold X. Then
for each 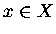 ,
the stabilizer G(x) acts on the tangent space TxX.
This also works if the groupoid G has a local transformation group
structure (union of transformation groupoids ,
the stabilizer G(x) acts on the tangent space TxX.
This also works if the groupoid G has a local transformation group
structure (union of transformation groupoids 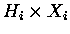 with compatibility).
with compatibility).
Question: Let G be a smooth groupoid. Can we get G(x)
to act on TxG(0)
without assuming the existence of a suitable choice of ``horizontal'' spaces
in TG over G(0)? |
Contributor: Jean
Renault
June 1999, Boulder
|
Preamble. Let us say that an étale groupoid G
is singly generated if there exists an open s-section 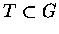 such that
such that 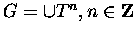 .
For example, the semi-direct product groupoids G(X,T)
associated to a local homeomorphism .
For example, the semi-direct product groupoids G(X,T)
associated to a local homeomorphism 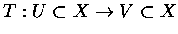 are singly generated. In particular, Cuntz-Krieger groupoids and AF groupoids
are singly generated. Let us say that a singly generated groupoid G
is uniquely singly generated if its only generators are T (or T-1
if T is a bisection). M. Boyle has shown that, whenever T
is an essentially transitive homeomorphism of a compact space X,
G(X,T)
is uniquely singly generated. This is also true when T is a homeomorphism
of a connected space X. On the other hand AF groupoids are not uniquely
singly generated.
are singly generated. In particular, Cuntz-Krieger groupoids and AF groupoids
are singly generated. Let us say that a singly generated groupoid G
is uniquely singly generated if its only generators are T (or T-1
if T is a bisection). M. Boyle has shown that, whenever T
is an essentially transitive homeomorphism of a compact space X,
G(X,T)
is uniquely singly generated. This is also true when T is a homeomorphism
of a connected space X. On the other hand AF groupoids are not uniquely
singly generated.
Question: Is there a general criterion for unique single generation? |
Contributor: Dmitriy
Rumynin
June 1999, Boulder
|
Question: Let G and H be Lie groupoids over a
smooth manifold X with respective Lie algebroids  and
and 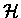 .
Given a Lie algebroid morphism .
Given a Lie algebroid morphism
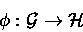
does there exist a groupoid map
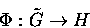
for a covering groupoid 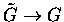 having the same Lie algebroid
having the same Lie algebroid 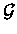 such that
such that 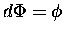 ? ?
Comment. It may be easy or known. If it is not, then I might
be able to apply my new technique to settle this. In fact, I had to integrate
a Lie algebroid map to a groupoid map in my work. I did it in the context
of algebraic geometry in characteristic p for certain groupoids
concentrated on the first Frobenius kernel of the diagonal. Not being an
analyst, I nevertheless believe that my technique would be applicable for
Lie groupoids as well.
Answer proposed by
Ieke Moerdijk
at March 1, 2001.
|
Contributor: Masamichi Takesaki
June 1999, Boulder
|
Question: Find a counterpart of the characteristic square of
a factor in the context of measured ergodic groupoids or Poisson manifolds. |
![]() .
.
![]() ,
the extension
,
the extension
![]() determine about (1) ?
determine about (1) ?
![]() having the same Lie algebroid
having the same Lie algebroid ![]() such that
such that ![]() ?
?