First day
Bucharest, Romania - 16th July, 1999

1

A set S of points from the plane will be called completely symmetric if it has at least three elements and fulfils the condition: for every distinct points A,B from S, the perpendicular bisector of the segment AB is an axis of symmetry for S.

Prove that if a completely symmetric set is finite then it consists of the vertices of a regular polygon.

2

Let n> 1 be a fixed integer. Find the least constant C such that the inequality

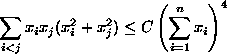
holds for any x 1 , x 2 , ... , x n greater than or equal to 0 .

For this constant, characterize the instances of equality.

3

Let n be an even positive integer. We say that two different cells of a n x n board are neighboring if they have a comon side. Find the minimal number of cells on the n x n board that must be marked so that any cell (marked or not marked) has a marked neighboring cell.

Each problem is worth 7 points.
Time: 4 1/2 hours.

Second day
Bucharest, Romania - 17th July, 1999

4

Find all pairs of positive integers (n,p) such that p is a prime, n <2p+1 ,and x p-1 is a divisor of (p-1) n +1 .

5

Two circles C 1 and C 2 touch internally the circle C in M and N and the center of C 2 is on C 1. The common chord of the circles C 1 and C 2 intersects C in A and B. MA and MB intersect C 1 in P and Q. Prove that C 2 is tangent to PQ.

6

Find all the functions f from real numbers to real numbers which satisfy

f(x-f(y))=f(f(y))+xf(y)+f(x)-1

for all real numbers x,y .
Each problem is worth 7 points.
Time: 4 1/2 hours.